Unlocking Geometry's Secrets: The Power of Undefined Terms

10 Jun 2024
us
Emil

Geometry Foundations: Basics of Geometry and Undefined Terms

Have you ever wondered how mathematicians build entire systems of knowledge? In geometry, it all starts with the simplest, yet most profound concepts: the undefined terms.

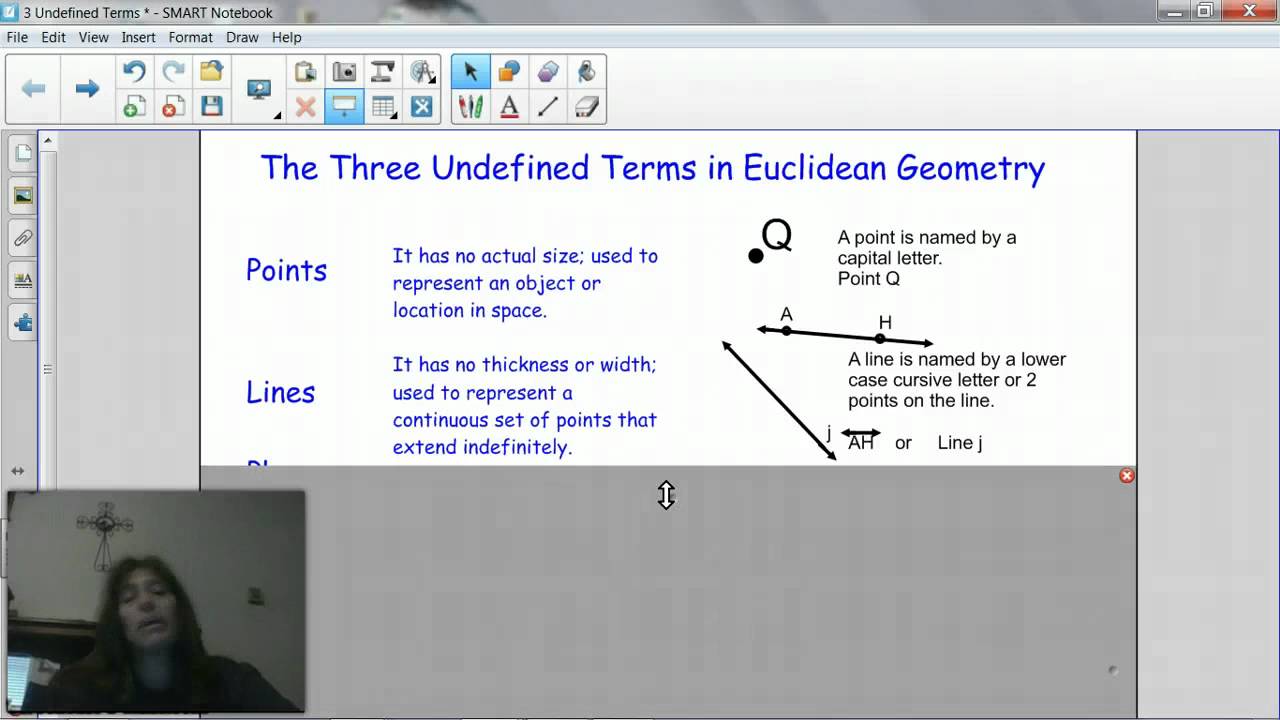
Imagine trying to describe a vast landscape without using words like "mountain" or "river." It seems impossible, right? Yet, in geometry, we begin with concepts so fundamental that they defy precise definition: the point, the line, and the plane.

These three undefined terms aren't just abstract ideas. They form the bedrock upon which we construct our understanding of shapes, sizes, and the very space we inhabit. Without them, geometry as we know it wouldn't exist.

Throughout history, mathematicians have grappled with the challenge of defining these fundamental concepts. Euclid, the father of geometry, recognized the need to build his system on a foundation of self-evident truths, his postulates. He chose to leave "point," "line," and "plane" undefined, relying instead on their intuitive understanding to build his geometric framework.

But this lack of formal definition doesn't mean these terms are vague or arbitrary. Instead, their power lies in their flexibility. We can think of a point as a tiny dot on a page, the tip of a sharpened pencil, or a location on a map. Similarly, a line can be represented by a taut string, the edge of a ruler, or the path of a ray of light. A plane might be visualized as a flat tabletop, a smooth sheet of paper, or even the surface of a still lake.

While we can provide examples and intuitive descriptions, we can't definitively define these terms without resorting to circular logic. For instance, defining a point as "an object with no dimensions" requires us to already understand the concept of "dimension."

The beauty of undefined terms lies in their ability to serve as building blocks. By combining them and applying logical reasoning, we can define more complex geometric figures and explore their relationships.

For example, using the undefined terms "point" and "line," we can define a line segment as the portion of a line that lies between two distinct points. Similarly, using the undefined terms "line" and "point," we can define an angle as the figure formed by two rays that share a common endpoint.

The undefined terms, despite their seemingly abstract nature, have real-world applications. Architects use their understanding of points, lines, and planes to design buildings. Engineers rely on these concepts to build bridges and other structures. Computer graphics and animation wouldn't be possible without the fundamental principles derived from these undefined terms.

Understanding these undefined terms is crucial for anyone seeking to unlock the wonders of geometry. They are the gateway to a world of shapes, patterns, and spatial reasoning, a world that underpins countless fields, from art and architecture to science and technology.

So, the next time you see a simple dot on a page, remember the profound concept it represents: the undefined yet powerful point, a foundational element of the language of geometry.