Imagine trying to calculate the exact amount of ingredients needed to double a recipe. Or figuring out how long it will take to travel a certain distance at a given speed. These scenarios, and countless others, can be represented and solved using the power of linear equations. But what exactly are these equations, and how can understanding them empower us to solve real-world problems?
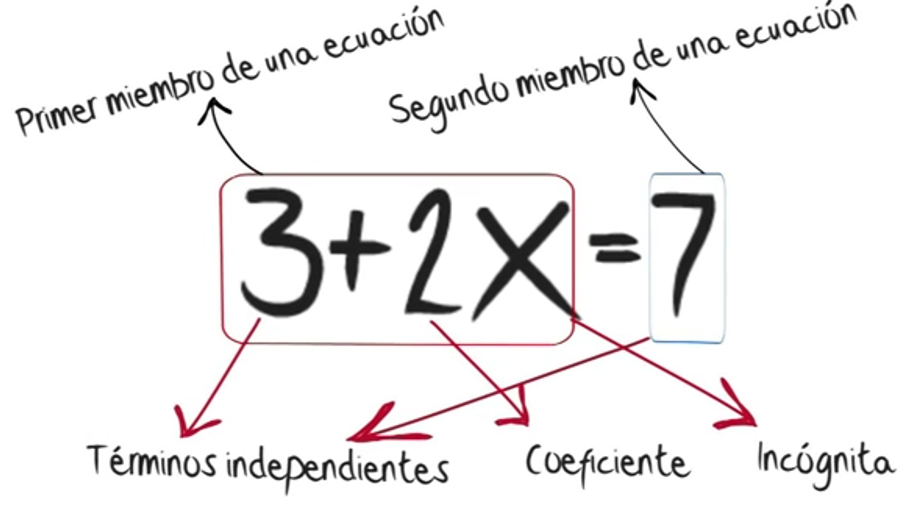
In essence, linear equations are mathematical expressions that represent a relationship between a variable and known numbers. The term "linear" refers to the fact that these equations graph as straight lines. The simplest form of a linear equation includes an unknown variable, typically represented by the letter 'x', and constants, which are fixed numerical values.
The history of linear equations can be traced back thousands of years to ancient civilizations like the Babylonians and Egyptians. They used these equations for practical purposes like dividing land and calculating trade. Over the centuries, mathematicians like Diophantus and al-Khwarizmi made significant contributions to the development of algebra, further solidifying the importance of linear equations in the realm of mathematics.
One of the main issues linear equations address is the problem of finding an unknown quantity when we know its relationship to other quantities. For example, imagine you're trying to determine the price of a single apple when you know that six apples cost $3. This problem can be easily represented and solved using a linear equation.
The beauty of linear equations lies in their simplicity and wide-ranging applications. They serve as the foundation for various mathematical concepts, including calculus, statistics, and linear algebra. From physics and engineering to economics and computer science, linear equations play a crucial role in modeling and solving real-world problems across countless fields.
Let's consider a simple example: 2x + 5 = 11. In this equation, 'x' is our unknown variable. To solve for 'x', we aim to isolate it on one side of the equation. We can achieve this by subtracting 5 from both sides (2x = 6) and then dividing both sides by 2 (x = 3). This simple process allows us to determine the value of the unknown variable 'x'.
Advantages and Disadvantages of Linear Equations
| Advantages | Disadvantages |
|---|---|
| Simple to understand and solve | Limited in representing complex relationships |
While linear equations are incredibly versatile, it's essential to recognize that not all real-world relationships can be accurately modeled by a straight line. In such cases, more complex mathematical models become necessary.
To conclude, linear equations provide a fundamental framework for understanding relationships between variables and solving for unknown quantities. Their applications extend far beyond the realm of mathematics, impacting fields like science, engineering, finance, and everyday life. By grasping the concepts of linear equations, we equip ourselves with a powerful tool for problem-solving and analytical thinking.
cuales son las ecuaciones de primer grado - Trees By Bike
cuales son las ecuaciones de primer grado - Trees By Bike
cuales son las ecuaciones de primer grado - Trees By Bike
cuales son las ecuaciones de primer grado - Trees By Bike
cuales son las ecuaciones de primer grado - Trees By Bike
cuales son las ecuaciones de primer grado - Trees By Bike
cuales son las ecuaciones de primer grado - Trees By Bike
cuales son las ecuaciones de primer grado - Trees By Bike
cuales son las ecuaciones de primer grado - Trees By Bike
cuales son las ecuaciones de primer grado - Trees By Bike
cuales son las ecuaciones de primer grado - Trees By Bike
cuales son las ecuaciones de primer grado - Trees By Bike
cuales son las ecuaciones de primer grado - Trees By Bike
cuales son las ecuaciones de primer grado - Trees By Bike
cuales son las ecuaciones de primer grado - Trees By Bike