Unlocking the Secrets of 45: Exploring its Factors and Divisors

26 Jun 2024
us
Emil

Ever wondered about the hidden building blocks of numbers? Numbers like 45 might seem simple at first glance, but lurking beneath the surface is a world of factors and divisors waiting to be discovered. Understanding the factors of a number opens up a deeper understanding of its properties and relationships with other numbers. So, let's embark on a journey to uncover the secrets of 45 and its divisors.

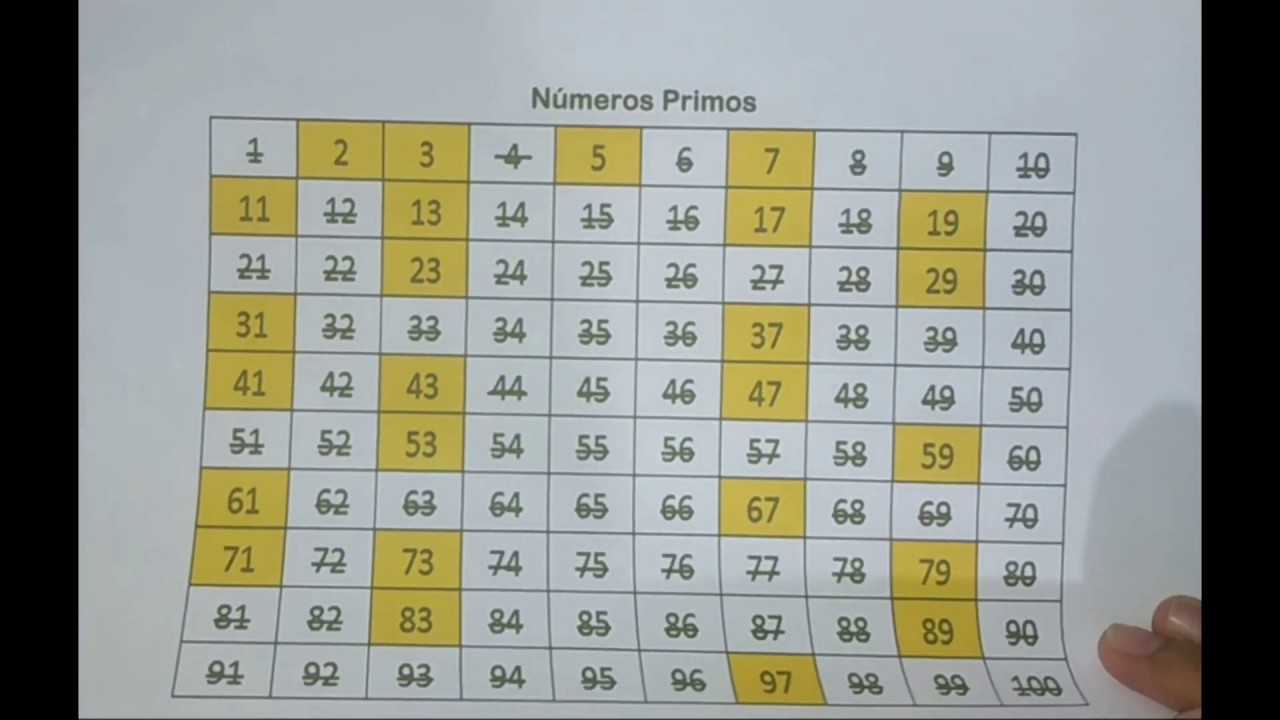
The question "quais os divisores de 45" translates from Portuguese to "what are the divisors of 45?" This seemingly simple question is the key to unlocking a deeper understanding of the number 45 within the field of mathematics. By exploring the divisors of 45, we gain insight into its divisibility, its prime factorization, and its potential uses in various mathematical contexts.

Factors, or divisors, are whole numbers that divide evenly into another number. For example, 3 is a factor of 45 because 45 divided by 3 equals 15 with no remainder. Finding all the divisors of a number helps us break it down into its fundamental components. This process is crucial for understanding concepts like greatest common divisors and least common multiples, which are essential tools in number theory and other branches of mathematics.

The concept of divisors dates back to ancient civilizations who studied the properties of numbers. Understanding divisibility was crucial for tasks like dividing land, distributing resources, and developing calendars. Today, the concept of divisors remains fundamental to modern mathematics, computer science, and cryptography. Identifying the prime factors of very large numbers plays a critical role in securing online transactions and protecting sensitive information.

The factors of 45 are 1, 3, 5, 9, 15, and 45. These numbers are significant because they perfectly divide 45 without leaving any remainder. This understanding allows us to simplify fractions, solve equations, and analyze patterns involving the number 45. By knowing the divisors of 45, we unlock its hidden structure and gain a deeper appreciation for its place within the numerical landscape.

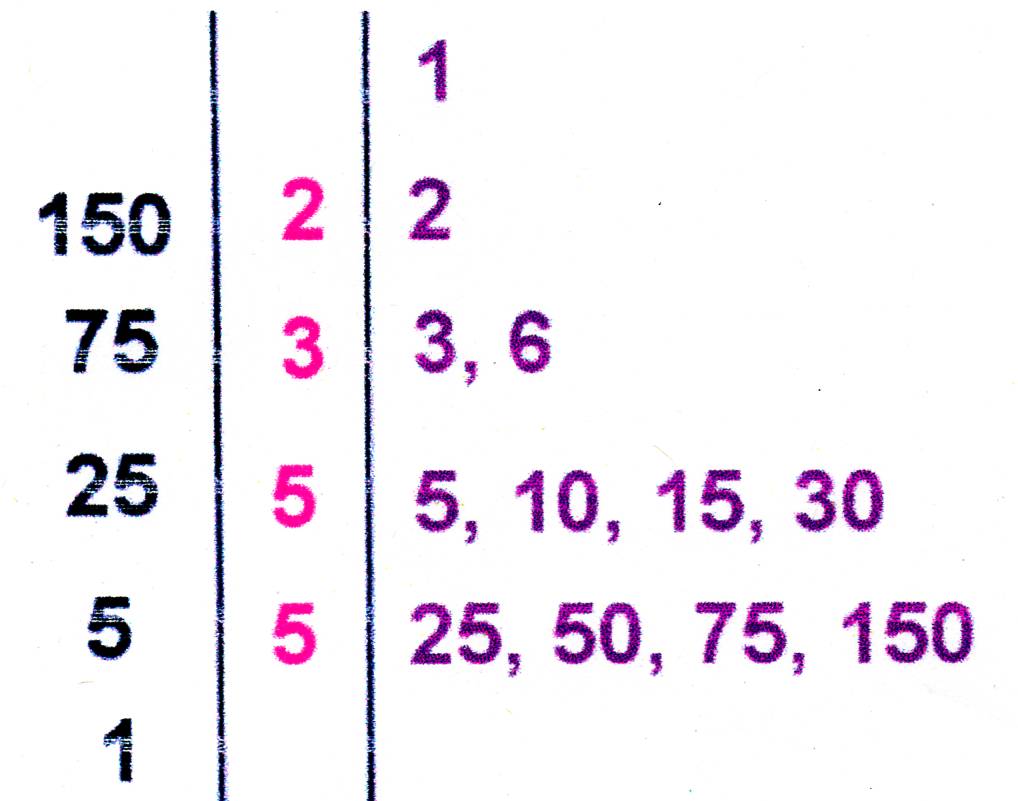
Finding the factors of a number like 45 can be beneficial in several ways. Firstly, it improves our understanding of prime numbers and prime factorization. 45 can be expressed as 3 x 3 x 5, showing the importance of the prime numbers 3 and 5 in its composition. Secondly, it helps in simplifying fractions involving 45. Knowing the factors allows us to reduce fractions like 45/75 to their simplest form. Lastly, it aids in solving mathematical problems involving divisibility and multiples, which are common in various fields like computer science and engineering.

To find the factors of 45, we can start by dividing 45 by 1, then 2, 3, and so on. If the division results in a whole number, that number is a factor. For example, 45/1 = 45, 45/3 = 15, and 45/5 = 9. Therefore, 1, 3, 5, 9, 15, and 45 are the factors of 45.

Advantages and Disadvantages of Working with Divisors

While working with divisors has many benefits in simplifying calculations and understanding number relationships, it can sometimes be computationally intensive for extremely large numbers.

Best practices for working with divisors include starting with the smallest divisors (1 and the number itself) and then checking divisibility by prime numbers. This systematic approach ensures that no factors are missed.

Frequently asked questions about divisors include: What is a divisor? How do you find divisors? What is the difference between a factor and a divisor? What is the greatest common divisor? What is the least common multiple? What are the applications of divisors? How are divisors used in cryptography? How are divisors relevant to prime factorization? These questions highlight the importance and relevance of divisors in various mathematical contexts.

In conclusion, understanding "quais os divisores de 45," or what are the divisors of 45, is much more than a simple math problem. It's about delving into the fundamental building blocks of numbers and exploring their interconnections. The divisors of 45, namely 1, 3, 5, 9, 15, and 45, provide crucial insights into the number's properties and relationships. This knowledge is essential for various mathematical operations, from simplifying fractions to solving complex equations. By understanding the factors of a number, we unlock a deeper appreciation for the intricate world of mathematics and its practical applications. So, the next time you encounter a number, take a moment to consider its divisors – you might be surprised by the secrets they reveal.