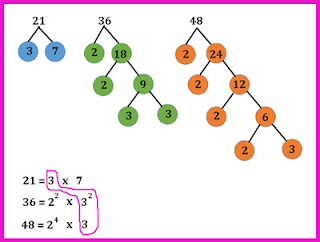
Numbers have always fascinated humanity. From the ancient Greeks pondering prime numbers to modern mathematicians grappling with complex equations, the quest to understand numbers continues. Today, we're going to explore two fundamental concepts in the realm of mathematics: the Least Common Multiple (KPK) and the Greatest Common Factor (FPB). While these terms might sound a bit technical, they are actually quite approachable and play a crucial role in various aspects of math, from simplifying fractions to solving real-world problems.
Imagine baking a cake for a large gathering. You have one recipe that yields 12 servings and another that makes 18. What's the smallest number of servings you can bake from both recipes without having any leftovers? This is where the concept of KPK comes in handy. KPK, or the Least Common Multiple, is the smallest positive integer that is divisible by both 12 and 18. In this case, the KPK is 36, meaning you could bake 3 batches of the first recipe and 2 batches of the second to get 36 servings.
Now, let's say you're dividing a rectangular piece of fabric into smaller squares for a quilting project. You want to use the largest possible squares to minimize waste. If the fabric measures 24 inches by 36 inches, the largest square you can cut has sides measuring the FPB of 24 and 36. FPB stands for the Greatest Common Factor, which is the largest number that divides evenly into both 24 and 36. In this case, the FPB is 12, so you can cut 12-inch squares.
The origins of KPK and FPB can be traced back to ancient Greece. Mathematicians like Euclid, known for his seminal work "Elements," laid the foundation for understanding these concepts. Euclid's algorithm, a method for finding the FPB of two numbers, is still widely used today. These concepts were not mere intellectual curiosities. They were essential tools for astronomy, music theory, and everyday life.
In our technology-driven world, KPK and FPB might seem less relevant. However, they still form the backbone of many mathematical operations. From simplifying fractions and working with ratios to cryptography and computer programming, the applications of KPK and FPB remain surprisingly vast. Understanding these fundamental concepts not only strengthens our mathematical foundation but also equips us to tackle a wide range of problems, both in academic and practical settings.
Advantages and Disadvantages of Calculating KPK and FPB
While the concepts of KPK and FPB are straightforward, let's delve into their advantages and potential drawbacks:
| Feature | Advantages | Disadvantages |
|---|---|---|
| Calculation | Straightforward methods using factorization or listing multiples. | Can become computationally intensive for very large numbers. |
| Applications | Widely used in various mathematical operations and real-world scenarios. | May not be directly applicable to every mathematical problem. |
| Conceptual Understanding | Enhances understanding of number theory and relationships between numbers. | May require some effort to grasp for beginners. |
Best Practices for Working with KPK and FPB
Here are some best practices to make working with KPK and FPB more efficient:
- Start with Factorization: Breaking down numbers into their prime factors can significantly simplify the process of finding KPK and FPB.
- Use Euclid's Algorithm for FPB: This efficient algorithm can help find the FPB even for large numbers.
- Look for Patterns: Recognizing patterns in numbers and their factors can often lead to quicker solutions.
- Practice Regularly: Consistent practice with different numbers and problem-solving scenarios strengthens understanding and improves efficiency.
- Utilize Online Resources: Several websites and apps offer KPK and FPB calculators and practice problems.
In conclusion, while the terms KPK and FPB might seem like relics from our math textbooks, their relevance extends far beyond the classroom. These fundamental concepts, rooted in ancient mathematics, continue to play a vital role in various fields, from everyday calculations to complex algorithms. By understanding and mastering KPK and FPB, we not only enhance our mathematical literacy but also equip ourselves with powerful tools to solve problems, make informed decisions, and appreciate the elegance of numbers in our world.
Cara Menentukan FPB dan KPK dengan Mudah dengan Tabel dan Pohon Faktor - Trees By Bike
cara cari kpk dan fpb - Trees By Bike
Cara Menentukan KPK dan FPB dari 50, 72, dan 90 - Trees By Bike
Cara Menentukan FPB dan KPK dengan Mudah dengan Tabel dan Pohon Faktor - Trees By Bike
Cara Mencari FPB Dan KPK dengan Tabel - Trees By Bike
Cara Mencari KPK dan FPB Lengkap dengan Contoh Soalnya - Trees By Bike
2 Cara Mencari KPK dan FPB Dengan Tabel, Kenali Tekniknya! - Trees By Bike
Cara Mencari FPB Dan KPK Beserta Contohnya Terlengkap - Trees By Bike
Cara Mencari KPK dan FPB Lengkap dengan Contoh Soalnya - Trees By Bike
30 Cara Menentukan Fpb Dan Kpk Dengan Pohon Faktor - Trees By Bike
Mengenal KPK dan FPB - Trees By Bike
Cara paling Mudah Mencari FPB dan KPK ~ Juragan Les - Trees By Bike
Cara Mencari FPB dan KPK dengan Cepat - Trees By Bike
Fpb Dari 8 Dan 12 Menggunakan Pohon Faktor - Trees By Bike
Foto : Perbedaan FPB dan KPK - Trees By Bike