Have you ever stopped to appreciate the elegance and ubiquity of a square? From the tiles on your floor to the pixels on your screen, squares are fundamental geometric shapes that surround us. While they might seem simple at first glance, their properties have fascinated mathematicians, architects, and artists for centuries.
In this exploration of squares, we'll delve into their fascinating history, uncover their unique characteristics, and discover how they influence various aspects of our lives. Whether you're a math enthusiast, a design aficionado, or simply curious about the world around you, understanding squares can offer a new perspective on geometry and its applications.
The concept of a square has existed for as long as humans have been able to perceive shapes. Ancient civilizations incorporated squares into their architecture, recognizing their structural stability and aesthetic appeal. The Great Pyramid of Giza, for instance, features a square base, showcasing the significance of this shape in ancient Egyptian architecture.
Over time, mathematicians rigorously defined the square, establishing its properties as a quadrilateral with four equal sides and four right angles. This precise definition paved the way for its use in various mathematical fields, including geometry, algebra, and trigonometry. The Pythagorean theorem, for example, highlights the relationship between the sides of a right triangle, which can be easily visualized and understood using squares.
Today, squares extend far beyond the realm of mathematics. They are integral to art and design, providing a sense of balance, stability, and order. From the grid-like layouts of modern websites to the precise compositions of abstract paintings, squares offer a versatile tool for visual communication. Their simplicity also makes them easy to replicate and manipulate, leading to their widespread use in fields like computer graphics and digital imaging.
Advantages and Disadvantages of Squares
| Advantages | Disadvantages |
|---|---|
| Simplicity and ease of construction | Lack of dynamic shape compared to other polygons |
| Structural stability and balance | Can appear monotonous in design if overused |
| Versatility in various applications | Limited in representing organic or irregular shapes |
Let's explore some best practices when working with squares:
1. Grid Systems in Design: Squares form the foundation of many grid systems used in graphic design, web design, and photography. These grids help create visual hierarchy, balance elements, and guide the viewer's eye.
2. Tessellations in Art: Squares are one of the three regular polygons that can tessellate, meaning they can fit together without gaps or overlaps. This makes them ideal for creating intricate patterns and designs in mosaics, tilework, and textiles.
3. Pixel Art and Digital Images: Digital images are composed of tiny squares called pixels. Understanding the concept of squares is crucial for image editing, resolution, and the creation of pixel art.
4. Area Calculation: The simple formula for calculating the area of a square (side x side) makes it a fundamental concept in geometry and everyday measurements.
5. Understanding Square Roots: The concept of a square root is directly related to squares. Finding the square root of a number means finding the side length of a square with an area equal to that number.
Here are some real-world examples of squares in action:
1. Chessboard: The classic chessboard is a prime example of a square grid used for a strategic game.
2. Floor Tiles: Square tiles are a popular choice for flooring due to their ease of installation and ability to create a clean, uniform look.
3. Windows: Many windows are square-shaped, providing a balanced and symmetrical view of the outside world.
4. Social Media Photos: Platforms like Instagram often utilize square image formats for a visually appealing and consistent feed.
5. City Planning: Grid-based city layouts, often incorporating square blocks, are common in urban planning, promoting organization and efficient navigation.
While squares offer numerous advantages, there are also some challenges to consider:
1. Monotony in Design: Overusing squares in design can lead to a monotonous and uninteresting visual experience. It's essential to balance squares with other shapes and elements.
2. Limitation in Representing Organic Shapes: Squares are not well-suited for depicting organic or irregular shapes found in nature. Other geometric figures may be more appropriate for these purposes.
3. Structural Limitations: While squares offer stability, they might not always be the most efficient shape for certain structures. Architects and engineers often explore a variety of shapes to optimize strength and material usage.
Let's address some common questions about squares:
1. What is the difference between a square and a rectangle? A square is a special type of rectangle where all four sides are equal.
2. How do you find the perimeter of a square? The perimeter of a square is found by adding up the lengths of all four sides. Since all sides are equal, the formula is simply 4 times the length of one side.
3. Can a square be considered a rhombus? Yes, a square is a special type of rhombus where all angles are right angles.
4. What is the significance of squaring a number? Squaring a number means multiplying it by itself. It has applications in various mathematical concepts, such as calculating areas and solving equations.
5. How are squares used in computer programming? Squares and their properties are utilized in various programming tasks, such as graphics rendering, game development, and algorithm design.
6. What is a perfect square? A perfect square is a number that can be obtained by squaring an integer. For example, 9 is a perfect square because it is the result of 3 x 3.
7. How do you find the diagonal of a square? The diagonal of a square can be found using the Pythagorean theorem or by multiplying the side length by the square root of 2.
8. What is the difference between area and perimeter? Area refers to the space enclosed within a two-dimensional shape, while perimeter is the total distance around the outside of the shape.
Here are some tips and tricks related to squares:
- Remember that all squares are rectangles, but not all rectangles are squares.
- When working with grids in design, use squares to create a sense of order and balance.
- Explore the concept of square roots to gain a deeper understanding of mathematical relationships.
In conclusion, squares are more than simple geometric shapes. They are fundamental building blocks in mathematics, design, art, and the world around us. From the tiles beneath our feet to the pixels illuminating our screens, squares are a testament to the elegance and power of simple geometry. By understanding their properties, we unlock a deeper appreciation for the role they play in various aspects of our lives, from the practical to the profound. So, the next time you encounter a square, take a moment to appreciate its simplicity, its versatility, and the countless ways it shapes our world.
segi empat sama in english - Trees By Bike
Mengenal Berbagai Jenis Segitiga Berdasarkan Sisi dan Sudut Matematika - Trees By Bike
Jenis Jenis Segi Empat Ingatwebku - Trees By Bike
Rumus Keliling Segi Empat Sama Sisi - Trees By Bike
Perbedaan Segi Banyak Beraturan Dan Tidak Beraturan - Trees By Bike
Segitiga Sama Kaki Rumus Sudut Sifat Luas Dan Contoh Soal - Trees By Bike
Foto : Soal dan Jawaban Sifat - Trees By Bike
Apakah Jenis Gabungan Sudut Pada Setiap Jenis Segi Empat Mempunyai - Trees By Bike
rumus volume prisma segi empat sama sisi Archives - Trees By Bike
Pin on Quick Saves - Trees By Bike
segi empat sama in english - Trees By Bike
math: Bentuk dan ruang - Trees By Bike
segi empat sama in english - Trees By Bike
Logo Bahasa Inggris, desain, sudut, bahasa Inggris, segi empat png - Trees By Bike
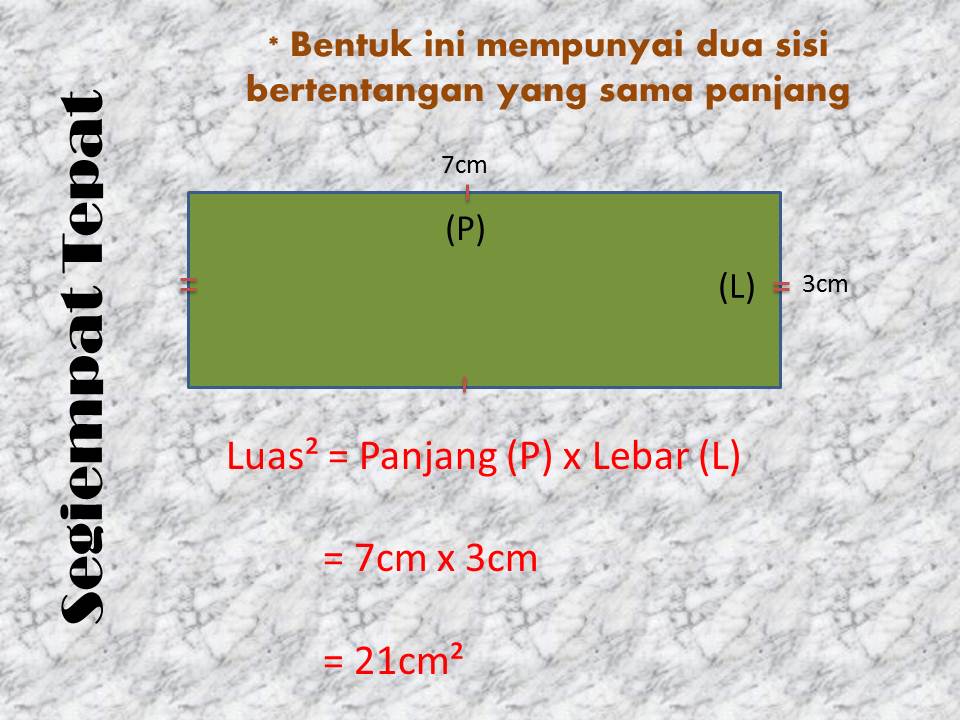
Rumus Luas Segi Empat Tepat Cara Menghitung Rumus Luas Dan Keliling - Trees By Bike