Tame Your AC Circuits with Phasor Power!

15 May 2024
us
Emil

Ever wonder how electricity actually *does* that whole alternating current thing? Direct current is simple enough – electrons flowing in a straight line, like water down a pipe. But AC? It's a bit wilder, like a tide that ebbs and flows. That's where phasors come in, giving us a powerful tool to understand and analyze these oscillating electrical waves.

Imagine trying to track a kid on a swing. Its position is constantly changing – up, down, up, down. Describing this motion with just instantaneous values is a headache. But what if you could represent this oscillating motion with a single, rotating arrow? That's the essence of a phasor: a rotating vector that represents a sinusoidal quantity (like voltage or current) in an AC circuit.

Instead of wrestling with messy trigonometric functions, phasors transform complex AC circuit analysis into simple vector addition and subtraction. They allow us to visualize the relationship between voltage and current in circuits with inductors and capacitors, components that react dynamically to changing currents. This simplification unlocks a deeper understanding of how AC circuits actually behave.

The beauty of phasor analysis lies in its ability to represent sinusoidal quantities with their magnitude and phase. The magnitude corresponds to the peak value of the sinusoid, while the phase represents its shift in time relative to a reference. This elegant representation makes complex AC circuit analysis manageable, allowing engineers to design and optimize everything from power grids to your phone charger.

Understanding phasors is essential for anyone working with AC circuits, from electrical engineers to hobbyists. They provide a practical and efficient method for analyzing complex circuits, predicting circuit behavior, and ensuring efficient power delivery. This knowledge empowers you to confidently tackle AC circuit problems, whether you’re designing a new circuit or troubleshooting an existing one.

The concept of phasors emerged in the late 19th century as engineers wrestled with the complexities of AC power systems. Charles Proteus Steinmetz, a brilliant mathematician and electrical engineer, is widely credited with popularizing the use of phasor diagrams for AC circuit analysis. His work greatly simplified the design and analysis of these increasingly complex systems, paving the way for the widespread adoption of AC power.

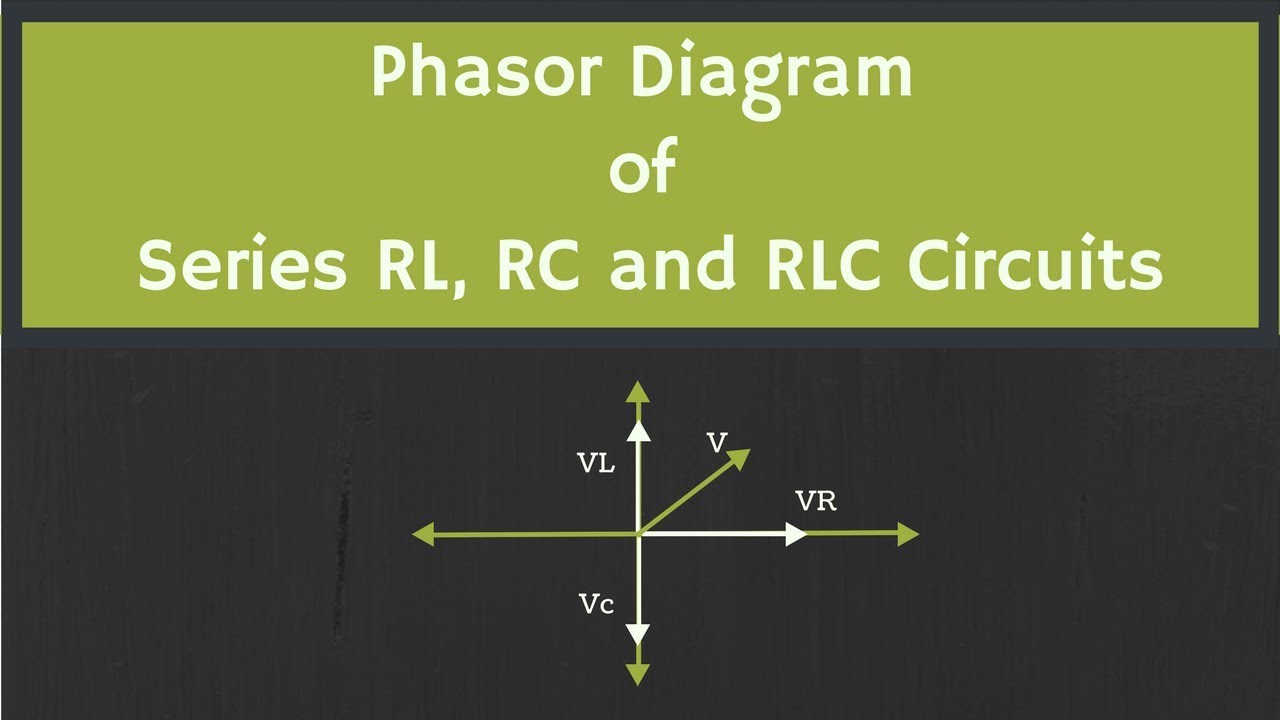
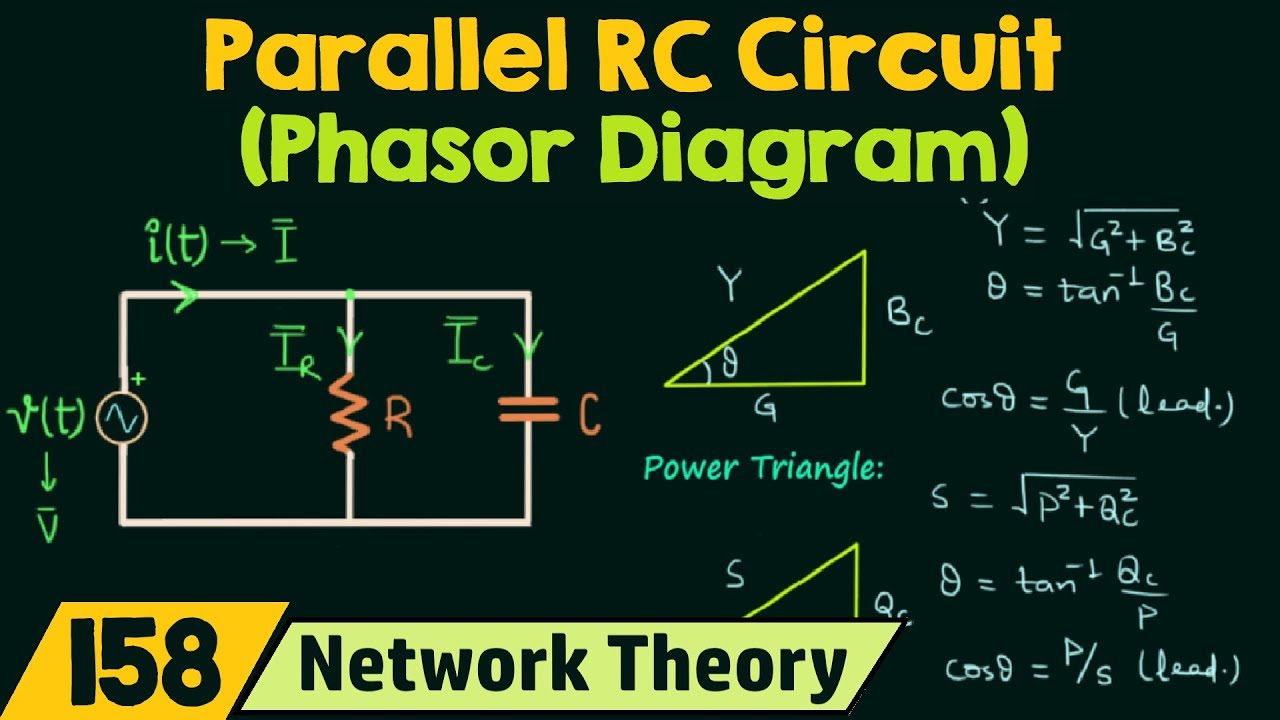
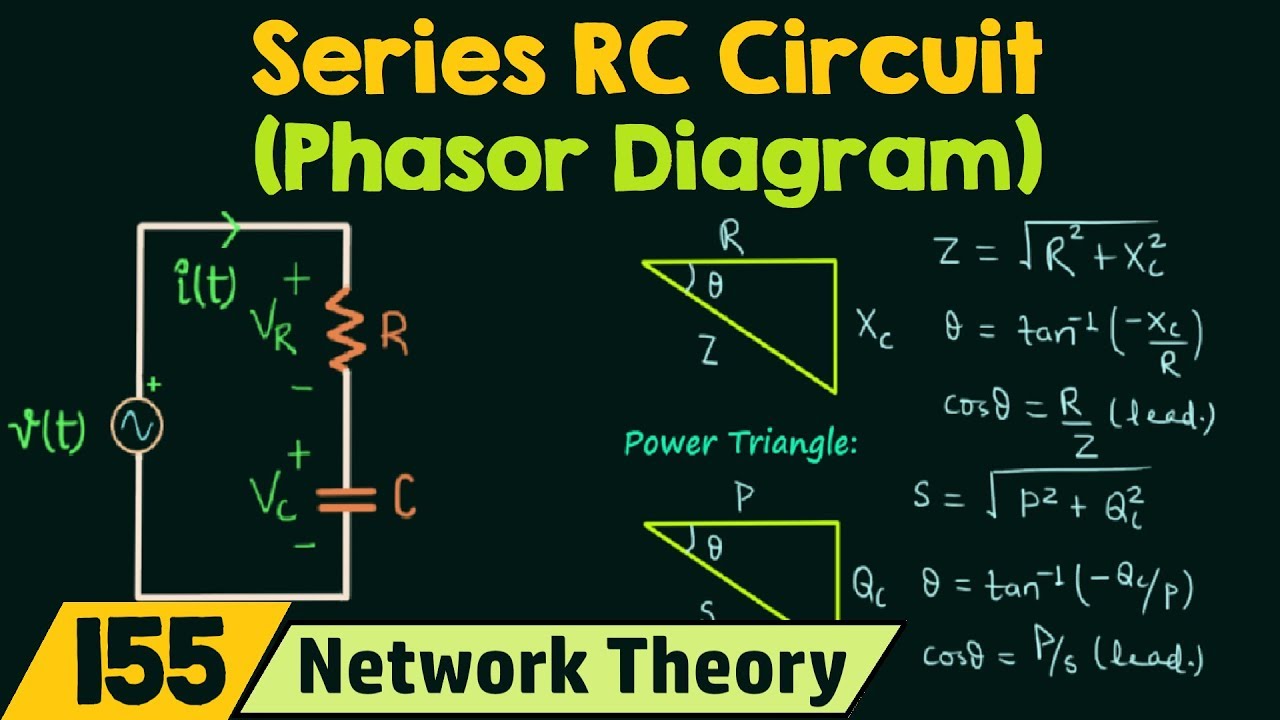
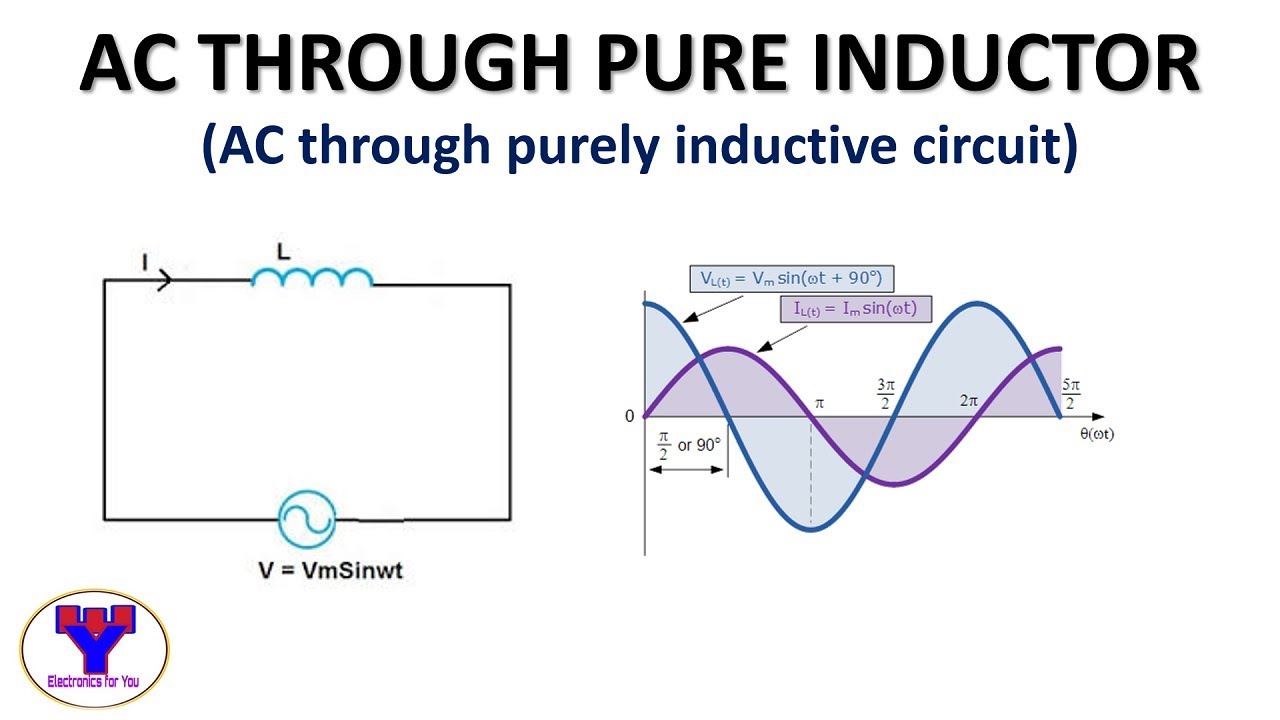
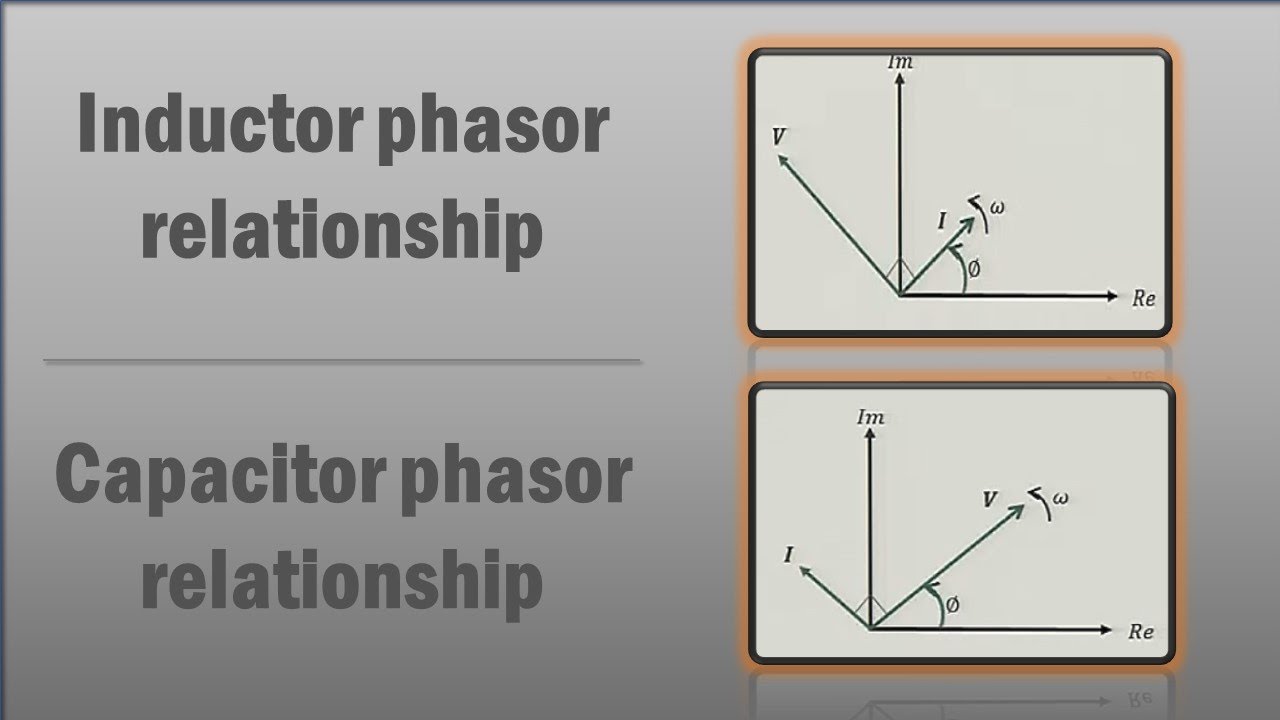
Phasors are invaluable for understanding the behavior of AC circuits containing reactive components like inductors and capacitors. These components store and release energy, causing phase shifts between voltage and current waveforms. Without phasors, analyzing these circuits would involve complex differential equations. Phasors transform these equations into algebraic ones, greatly simplifying calculations.

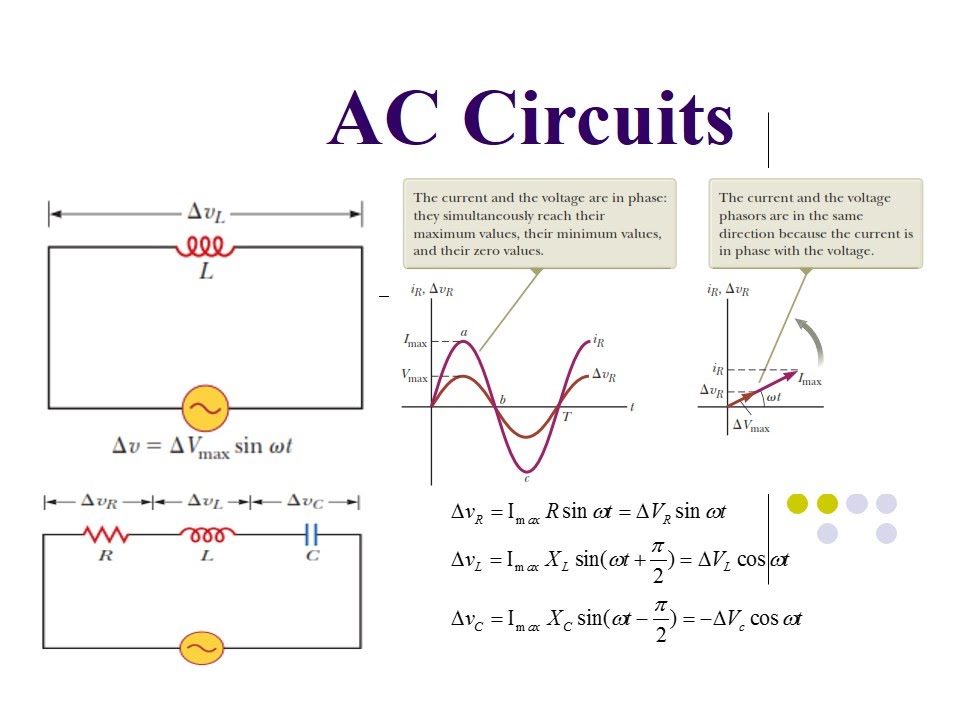
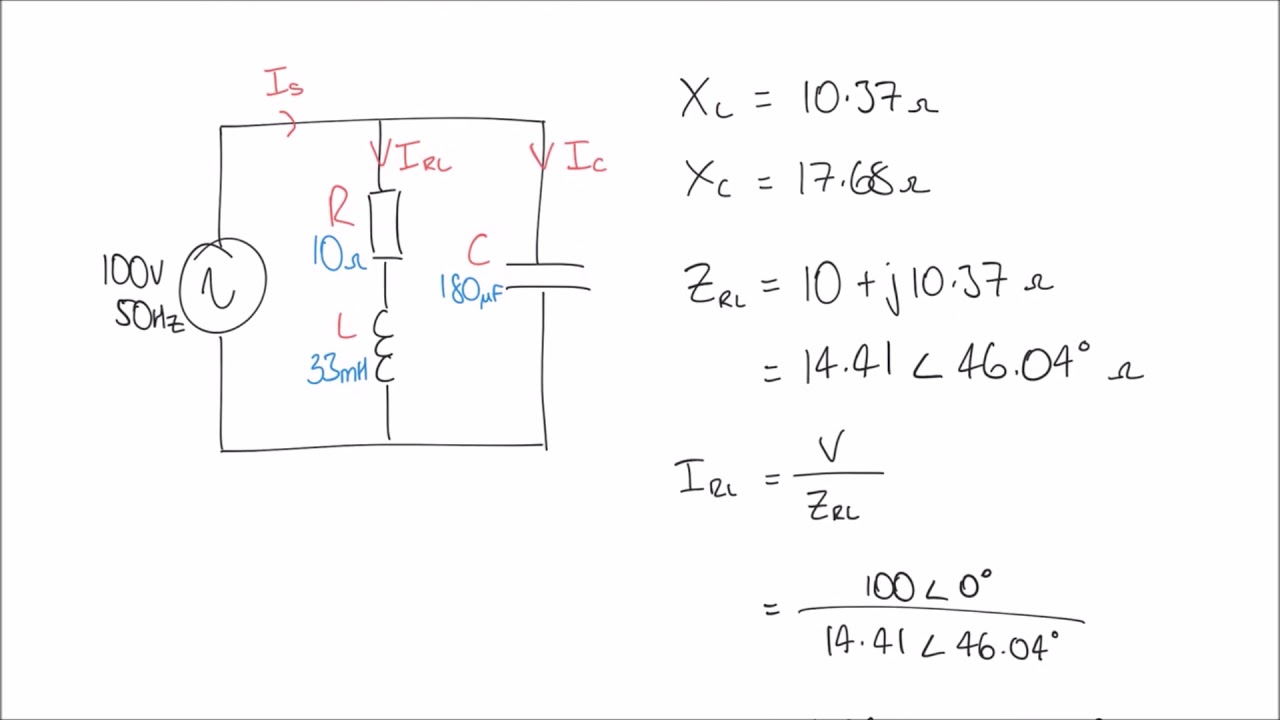
A phasor is a complex number that represents the magnitude and phase of a sinusoidal quantity. For example, a voltage phasor V = 10∠30° represents a voltage with a peak value of 10 volts and a phase angle of 30 degrees. The phase angle indicates how much the voltage waveform leads or lags a reference waveform.

Benefits of using phasors include: 1) Simplified Calculations: Phasors turn complex differential equations into simpler algebraic equations. 2) Clear Visualization: Phasor diagrams provide a visual representation of the relationships between voltages and currents in AC circuits. 3) Efficient Circuit Analysis: Phasors allow for efficient analysis of complex AC circuits, enabling engineers to design and optimize circuits for various applications.

To analyze an AC circuit using phasors, convert all sinusoidal voltages and currents into their phasor equivalents. Then, use basic vector addition and subtraction to analyze the circuit. Finally, convert the resulting phasor back into its time-domain representation to obtain the actual waveform.

Advantages and Disadvantages of Phasor Analysis

Advantages	Disadvantages
Simplified calculations	Only applicable to sinusoidal waveforms
Visual representation of circuit behavior	Can be challenging to visualize for complex circuits
Efficient analysis of complex circuits	Requires understanding of complex numbers

Best practices for phasor analysis include: 1) Ensure all sources operate at the same frequency. 2) Clearly define the reference phasor. 3) Use appropriate software tools for complex circuits. 4) Double-check calculations for accuracy. 5) Understand the limitations of phasor analysis.

Challenges in phasor analysis often arise when dealing with non-sinusoidal waveforms or circuits with non-linear components. Solutions involve advanced techniques like Fourier analysis or numerical simulations.

Frequently Asked Questions: 1) What is a phasor? 2) Why are phasors used? 3) How are phasors represented? 4) How do you convert a sinusoid to a phasor? 5) How do you add phasors? 6) What are the limitations of phasor analysis? 7) What are some real-world applications of phasors? 8) Where can I learn more about phasors?

Tips and tricks for phasor analysis include using phasor diagrams to visualize circuit behavior and utilizing software tools for complex calculations. Understanding the relationship between phasors and impedance is crucial for effective circuit analysis.

In conclusion, phasors are an invaluable tool for anyone working with AC circuits. They provide a simplified and efficient method for analyzing complex circuits, allowing for better design and optimization. Mastering phasor analysis opens doors to understanding the dynamic world of AC power, from household appliances to large-scale power systems. By embracing the power of phasors, you can unlock a deeper understanding of electrical engineering and its practical applications. Whether you're a seasoned engineer or just starting your journey, learning about phasors is an investment that will pay dividends in your understanding and ability to work effectively with AC circuits. Explore further resources, practice with examples, and unlock the power of phasor analysis today.